Mathematics
Time 3.00 Hrs. Class XI Marks 100
Aims & objectives-
The general objectives and teaching mathematics at secondary stage are to help the learners to-
1. Apply mathmatical knowledge and skills to solve real life problems by developing abilities to.
2. Develop avarenoss of the need foe national unity and develop confidence for the campetiltive examination.
3. Consolidate the mathematical knowledge and skills acquired earlier.
4. Acquire knowledge and understanding of the terms and symbols, concept, principles, processe, profs etc.
5. Develop mastery of basic algebriaic skills.
6. Develop drawing skills.
7. Devlop the ability to articulate logically.
8. Develop necessary skills with modern tecnological devices such as calculaters computers etc.
9. Develop reverence and respect towards great mathematics particularly Indian mathematicians for their contribution to the field of mathematics.
10. Develop positive thinking.
--------------------------------------------------------------------------------------------------------------------
Units Topics Marks Periods
--------------------------------------------------------------------------------------------------------------------
1 Complex Numbers 05 09
2 (A) Special Simultaneous equation in three
variables and their solutions.
(B) Theory of Quadratic Equations. 05 09
3 Arithmetic Progression and
Harmonic Progression 10 05
4 Geometric Progression
and special series. 05
5 Determinants 05 05
6 Matrices 05 05
7 Cartesian Coordinates of points. 09
8 Straight line 15 09
9 Pair of lines 09
10 Circle 05 09
11 Conic Section 05 05
12 Trigonometric Functions 10 09
13 Trigonometrical identities,
graph and equations 09
14 Properties of triangle
and solution of triangles 05 09
15 Height and Distance 05 09
16 Statistics 05 09
17 Permutation and Combination 05 09
18 Mathematical Induction
and Binomial Theorem 05 09
19 (A) Linear Inequalites
(B) Linear Programming 05 09
20 Exponential and
Logarithms Series 05 09
Revision 20
Total: 100 180
--------------------------------------------------------------------------------------------------------------------
1. Complex Numbers: 5
Representations of complex numbers as points on a plane, Argand diagram (addition and multiplication of complex numbers Geometrically) Algebra of complex numbers. The real and the imaginary parts of complex numbers, modules
and argument of conjugate of complex numbers, square root of complex num bers, cube root and fourth root of unity.
Triangular in equality: 
and equality 
Polar representation of complex numbers. Statement of fundamental theorem of algebra, solution of quadratic equations in the complex number system.
2 . (A) Simultaneous Equation of three variables and their solutions 5
(B) Theory of quadratic equations
Existence of maximum two roots of a quadratic equations; discriminate and nature of roots, relation between the roots and the coefficient symmetric functions, Vedic method for solution of quadratic equation.
e. g. 
and their values.
Formation of quadratic for specified roots.
Introduction to quadratic in equation ax2+bx+c³ 0 and its solution by using number line and sign convention,
3. Arithmetic Series and Harmonic Series : (UNIT 3 & 4 - 10 Marks)
Definition, First term, common difference, nth term, arithmetic mean, sum of n terms . Relation of Harmonic series with arithmetic series, nth terms of harmonic series.
4. Geometric Series and Special Series:
Definition of geometric series, first terms, common ratio, nth term infinite geometric series sum of n terms of geometric series sum of n terms of infinite series, geometric mean, value of recurring decimal considered as geometric series values of special series ----------and arithmetic & geometric series.
5. Determinant 5
Determinant, minors and cofactors, expansion of determinants , properties and transformations of determinants. Application of determinants in computing the area. of a triangle (Note Cramer's Rule is not included).
6. Matrices 5
Matrices as a rectangular array of numbers. Types of matrices, equality of matrices, sum of matrices, multiplication of scalar with a matrix, Product of matrices and linear combination. Associative and distributive law, Commulative law not being valid, Trans pose , cofactors and inverse of a matrix, their algebra and properties, solution of linear equations of three variables by matrix method.
7. Cartesian Coordinates of Points (UNIT 7, 8 & 9 - 15 Marks)
Rectangular Cartision coordinates, plotting of points. (With coordinates). on a plane, Distance between two points, area of triangle, condition for collinearity of three points, section of line segment in specified ratio, Centroid and in centre of a triangle locus and their equations transformation of and origin and axes.
8. Straight Line
Slope of straight line equations of various types of straight lines;
(i) slope and intercept on y axis.
(ii) One Point slope form
(iii) Intercepts on both axes
(iv) Distance form (Parametric equation)
(v) Normal from origin form
General equations of straight line, intersection of two lines, angle between two lines, condition for lines to be parallel or perpendicular, conditions of concurrence of three lines, Distance of a line from a given point. Ortho centre and circumcentre of triangles. Equations of angle bisector of two lines.
9. Pair of Straight lines:
Family of lines, Equation of lines through the point of intersection of two lines.Homogenous equations of second degree in two variables combined equation of angle bisectors of a pairs of lines passing through origin, condition for the general equation of second degree in two variables to represent the pair of straight line, the coordinates of their point of intersection, angle between them. Condition for the lines to be parallel and perpendicular.
10. Circle : 5
Standard equation of circle, general equation of circle, centre and radius of circle.
Parametric equations of circle, equation of the circle when coordinates of the extremities of a diameter are given, intersection of a line with circle condition for a line to be a tangent, equation of a tangent through a given point when (i). The point is on the circle. (ii). The point is outside the circle; Position of a point with respect to a circle.
11. Conic Section 5
Introduction to the various curves such as circle, parabola, ellipse, hyperbola, pair of straight lines and a point, obtained by the section of a cone, standard equation of ellipse, parabola and hyperbola, the coordinates of their . foci and vertices, equation of directrix lotus rectum Focal distance, the position of a point with respect to parabola, ellipse and hyperbola.
12. Trigonometric Functions (UNIT 12 & 13 - 10 Marks)
Degree measure of angle, radian measure relation between radian and degrees value of Trigonometrical ratios of the angles 
limiting position and trigonometrically ratios for 0angle and 90angle based on simple logic. Reading of values of trigonometrically ratios of other angles (0angle to 90angle) using of trigonometrically tables. Trigonometrically identifies. Proof of 
Expressing trigonometric ratios of angle (-
) in terms of e.g. 
etc. Expression of the trigonometric ratios of the following angles in terms 
of trigonometric ratios of angle 
Proofs and application of the following formulas.
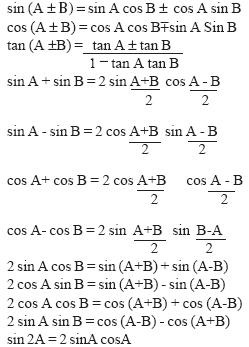
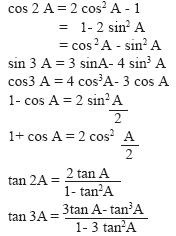
13. Trigonometrical Identities, graphs and equations:
Trigonometric identifies and conditional identifies (Related to angles of a triangle). Concept of the periodicity of trigonometric functions graphs of trigonometric functions such as.
y = sin x, y = a cos x, y = a tan bx, y = a sin (bx+c) etc.
Most general solutions of trigonometrical equations such as .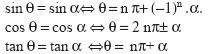 
etc. and their application.
14. Properties of triangle and solution of triangles
Relation between area of a triangle and circum radius
Solution of triangles when
a) Two angles and a side is given.
b) When two sides and included angle is given.
c) All the three sides are given.
d) When two sides and angle opposite to one of them is given.
15. Height and Distance 5
Problems involving height and distances (Two dimensional and three dimesional).
16. Statistics 5
Measure of central tendencies: Mean, Median and mode (Individual, grouped (i) inclusive (ii) Exclusive series). Direct and short cut (assumed mean) method mean deviation, dispersion, standard deviation variance, coefficient of variation (Individual , discrete and grouped). (continuous and discontineous groups). Direct method, short cut method (assumed
mean method).
17. Permutation and Combinations 5
Life history and centre tution of Mahavira Charya Law of counting, meaning of n , meaning of permutation' in reference to arrangement i.e npr and meaning of combination in terms of selection i.e, ncr , their applications, circular permutation etc.
18. Mathematical Induction and Binomial Theorem 5
Principle of mathematical induction in reference to natural numbers and their simple application. Proof of Binomial theorem (Positive integral) index using mathematical induction. Determination of general and particular term, Binomial theorem for any index ( with out proof), use of Binomial theorem in estimating approximate values, properties of Binomial coefficients.
19. (a) Linear Inequalities- 5
Linear inequalities, Algebraic Solutions of linear inequalities in are variable and their representation on the number line.
(B) Linear Programming- 5
Linear inequations in two variables and graph of their solutions set. Graph of solution set of system of linear inequation. Meaning of linear programming and its significance objective function, optimisation, isoprofit line etc. Convex Polygen (set) explanations of its properties mathematical formulation of linear programming problems and solution by graphical
method.
20. Exponential and Logarithmic Series 5
Infinite series for e, Proof of value of e lying between 2 and 3 i.e, 2<e<3 explanation of ex . Expanding log (1+x) and loge (1-x) as infinite series. Determination of logarithm of numbers using appropriate logarithmic series.
Note:- Use of vedic mathmatics at appropriti places as allternete methods of solvting problems.
Index : Madhya Pradesh Board Syllabus All Classes>>