Series OSS Code No. 65/1
MATHEMATICS
Time allowed : 3 hours Maximum Marks :100
General Instructions :
(i) All questions are compulsory.
(ii) The question paper consists of 29 questions divided into three sections A, B and C. Section A comprises of 10 questions of one mark each, Section B comprises, of 12 questions of four marks each and Section C comprises of 7 questions of six marks each.
(iii) All questions in Section A are to be answered in 1 word, 1 sentence or as per the exact requirement of the question. (iv) There is no overall choice. However, internal choice has been provided in 4 questions of four marks each and 2 questions of six marks each. You have to attempt only one of the alternatives in all such questions.
(v) Use of calculators is not permitted.
SECTION A
Questions number 1 to 10 carry 1 mark each.
1. If, f : R → R be defined by f(x) = (3 - x3)1/3, then find fof(x).
2. Write the principal value of sec-1(-2).
3. What positive value of x makes the following equal ?
4. Evaluate :
sec2 (7 - 4x) dx
5. Write the adjoint of the following matrix:
6. Write the value of the following integral:
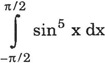
7. A is a square matrix of order 3 and |A| = 7. Write the value of |adj. A|.
8. Write the distance of the following plane from the origin:
2x-y+2z+1=0
9. Write a vector of magnitude 9 units in the direction of vector
10. Find λ if 
.
SECTION B
Questions number 11 to 22 carry 4 marks each.
11. A family has 2 children. Find the probability that both are boys, if it is known that
(i) at least one of the children is a boy,
(ii) the elder child is a boy.
12. Show that the relation S in the set A = 
given by S = {(a, b) : a, b ε Z, I a – b I is divisible by 4} is an equivalence relation. Find the set of all elements related to 1.
13. Prove the following
OR
14. Express the following matrix as the sum of a symmetric and skew symmetric matrix, and verify your result:
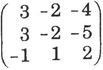
15. If 
find a vector . of magnitude 6 units which is parallel to the vector 
OR
Let 
and 
. Find a vector 
which is perpendicular to both 
.
16. Find the points on the line x + 2/ 3 = y + 1/2 = z – 3/ 2 at a distance of 5 units from the point P(1, 3, 3).
OR
Find the distance of the point P(6, 5, 9) from the plane determined by the points A(3, -1, 2), B(5, 2, 4) and C(-1, -1, 6).
17. Solve the following differential equation :
OR
Solve the following differential equation :
18. Show that the differential equation 
, is homogeneous and solve it.
19. Evaluate the following :
20. Evaluate the following :
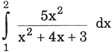
21. If y = ea sin-1 x, 
then show that
.
22. If 
.
SECTION C
Questions number 23 to 29 carry 6 marks each.
23. Using properties of determinants, prove the following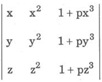 
= (1 + pxyz) (x – y) (y – z) (z – x)
OR
Find the inverse of the following matrix using elementary operations :
24. A bag contains 4 balls. Two balls are drawn at random, and are found to be white. What is the probability that all balls are white ?
25. One kind of cake requires 300 g of flour and 15 g of fat, another kind of cake requires 150 g of flour and 30 g of fat. Find the maximum number of cakes which can be made from 7.5 kg of flour and 600 g of fat, assuming that there is no shortage of the other ingradients used in making the cakes. Make it as an L.P.P. and solve it graphically.
26. Find the coordinates of the foot of the perpendicular and the perpendicular distance of the point P(3, 2, 1) from the plane 2x - y + z + 1 = 0. Find also, the image of the point in the plane.
27. Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y.
OR
Using integration, find the area of the triangle ABC, coordinates of whose vertices are A(4, 1), B(6, 6) and C(8, 4).
28. If the length of three sides of a trapezium other than the base is 10 cm each, find the area. of the trapezium, when it is maximum.
29. Find the intervals in which the following function is
(a) strictly increasing,
(b) strictly decreasing.