MATHEMATICS

ISC Question Paper XII (Commerce & Science Group) - 2009

General Instruction:

(i). Candidates are allowed additional 15 minutes for only reading the paper.

(ii). They must NOT start writing during this time

(iii). Section A - Answer Question 1 (compulsory) and five other questions. Section B and Section C - Answer two questions from either Section B or Section C.

(iv). All working, including rough work, should be done on the same sheet as, and adjacent to, the rest of the answers.

(v). The intended marks for questions or parts of questions are given in brackets []. Mathematical tables and squared paper are provided. Slide rule may be used.

SECTION – A

Q1.(i). If , Show that M(x) + M(y) = M(x+y).

(ii). The lines x- 2y + 6 = 0 and 2x - y - 10 = 0 intersect at the point A. Find the equation of the line making an angle 45 degree with the positive direction of the x-axis and passing through the point A.

(iii). Find the equations of the tangents to parabola   from the point (3, 8).

(iv). Find the derivative of sin with respect to .

(v). Evaluate the following  integral : .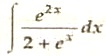

(vi). Evaluate the following limit : .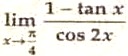

(vii). Two horses are considered for a race. The probability of selection of the first horse is 1/4 and that of the second is 1/3. What is the probability that :

       (a) both of them will be selected

       (b) only one of them will be selected

       (c) none of them will be selected.

(viii) The mean weight of 70 students in a class is 60 kg. The mean weight of the girls in the class is 53 kg and that of the boys is 70.5 kg. Find the number of girls in the class.

(ix) If   find the real numbers a and b. With these values of a and b, also find the modulus of a + ib.

(x) Solve the following differential equation :    .

 

Q2. (a) By using properties of determinants, prove that:                   5

               

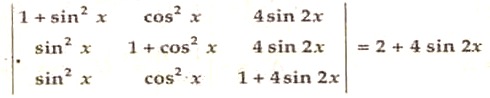
      (b) Solve the following linear equations using the matrix method :             5
                           x+y+z=9

                          2x+5y+7z=52

                          2x+y-z=0

Q3. (a) Prove that the following equation represents a pair of straight lines. Find their point of intersection and the angle between them :                    5

                                   

      (b) P, Q and R represent switches in 'on' positions and   represent switches in 'off' positions. Construct a switching circuit representing the polynomial   Use Boolean algebra to prove that the above circuit can be simplified to an expression in which, when P and R are 'on' or Q and R 'on', the light is on. Construct an equivalent circuit.                    5

Q4. (a) If   prove that :           5

                   

     (b) Using a suitable substitution find the derivative of   with respect to x.         5

Q5. (a) It is given that Rolle's theorem holds good for the function

at the point x = 4/3. Find the values of a and b.                5

      (b) A wire of length 20 m is available to fence off a flower bed in the form of a sector of a circle. What must be the radius of the circle, if we wish to have a flower bed with the greatest possible area ?                5

Q6. (a) (i) Evaluate:  log(tan x)dx.

            (ii) Evaluate  (x + 1/2)dx as a limit of a sum.

       (b) Draw a rough sketch of the curve + y = 9 and find the area enclosed by the curve, the x-axis and the the lines x + 1 = 0 and x – 2 = 0.

Q7. (a) An examination of 8 applicants for a clerical post was taken by a firm. The marks obtained by the applicants in the Reasoning and Aptitude tests and given below:

 

Applicant	A	B	C	D	E	F	G	H
Reasoning Test	20	28	15	60	40	80	20	12
Aptitude Test	30	50	40	20	10	60	30	30

Calculate the Spearman's coefficient of rank correlation from the data given above.       5

       (b) If the two regression lines of a vicariate distribution are 4x - 5y + 33 = 0 and 20x - 9y-107 = 0.

            (i) calculate x and Y, the arithmetic means of x and y respectively

            (ii) estimate the value of x when y = 7

            (iii) find the variance of y when ax = 3.           5

Q8. (a) Bag A contains 5 white and 4 black balls, and bag B contains 7 white and 6 black balls. One ball is drawn from the bag A and without noticing its colour, is put in the bag B. If a ball is then drawn from bag B, find the probability that it is black in colour.     5

     (b) An article manufactured by a company consists of two parts A and B. In the process of manufacture of part A, 9 out of 104 parts may be defective. Similarly, 5 out of 100 are likely to be defective in the manufacture of part B. Calculate the probability that the article manufactured will not be defective.            5

Q9. (a) If z= (13-5i)/(4-9i), Prove by using De Moivre’s theorem  that              5

       (b) Solve the following differential equestion for a particular solution. dy = (5x - 4y)dx , when y=0 and x=0.       5

SECTION B

Q10. (a) Find the equation of the plane which contains the line (x-1)/2 = (y+1)/(-1) = (z-3)/4 perpendicular to the plane x + 2y + z = 12.                      5

         (b) Find the equation of the sphere which passes through the circle   x+2y+2z=0 and whose centre lies on the plane 2x-y+z=1.               5

Q11. (a) Find the area of a parallelogram whose diagonals are determined by the vectors a = 3i+j-2k-and b = i-3j+4k.

        (b) (i) Prove by vector method that the diameter of a circle will subtend a right angle a t a point on its circumference.             2

            (ii) If a, b and c represent the position vectors of the points with co-ordinates (2,-10,2), (3, 1, 2) and (2, 1, 3) respectively, find the value of a x ( b x c) .               3

Q12. (a) The mean and variance of a binomial distribution are 4 and 2 respectively. Find the probability of at least 6 successes.            5

        (b) An insurance company insured 4000 doctors, 8000 teachers and 12000 engineers. The probabilities of a doctor, a teacher and an engineer dying before the age of 58 years are 0.01, 0.03 and 0.05 respectively. If one of the insured persons dies before the age of 58 years, find the probability that he is a doctor.          5

SECTION C

Q13. (a) A bill for Rs 84150 is drawn on 22nd April, 2002 at 11 months and is discounted on 11th January 2003. Find the banker's gain if the rate of interest is 10%.                 5

       (b) An iPod is purchased on installment basis, such that Rs 8000 is to be paid on the signing of the contract and four yearly installments of Rs 3000 each, payable at the end of the first, second, third and fourth years. If compound interest is charged at 5% per annum, what would be the cash price of the iPod ? [Take = 0.82271].            5

Q14. (a) A new cereal, formed of a mixture of bran and rice, contains at least 88 grams of protein and at least 36 milligrams of iron. Knowing that bran contains 80 grams of protein and 40 milligrams of iron per kilogram, and that rice contains 100 grams of protein and 30 milligrams of iron per kilogram, find the minimum cost of producing a kilogram of this new cereal if bran costs Rs 28 per kilogram and rice costs Rs 25 per kilogram.                5

        (b) The cost of manufacturing of certain items consists of Rs 1600 as overheads, Rs 30 per2 for x items produced. How item as the cost of the material and the labour cost Rs/100 many items must be produced to have a minimum-average cost ?                     5

Q15. (a) Calculate the index number for the year 2006 with 1996 as the base year by the weighted average of price relatives method from the following data.

Commodity	A	B	C	D	E
Weight	40	25	20	5	10
Price (Rs per unit) Year1996	32.00	80.00	1.00	10.20	4.00
Price (Rs per unit) Year 2006	40.00	120.00	1.00	15.36	3.00

     (b) A propeller costs Rs 180000 and its effective life is estimated to be 10 years. A sinking fund is created for replacing the propeller by a new model at the end of its life time, when its scrap realizes a sum of Rs 34000 only. The price of the new model is estimated to be 30% more than the price of the present one. What amount should be put into the sinking fund at the end of each year , if it accumulates at 4% per annum compound interest ? [Take (1.04) power 10 = 1.480].