Chapter – 8 Accounting Information & Its Applications

 

1. Chapter Introduction

2. Absorption Costing & Marginal Costing

3. Break Even Point & Marginal Cost

4. Utility of Marginal Costing

5. Marginal Costing: Advantages & Limitations

6. Practical Problems

 

 

1.    Chapter Introduction:

The cost of a product can be ascertained (using the different elements of cost) by Absorption or Marginal costing. In this chapter, we will discuss about the techniques of Absorption & Marginal costing.

Moreover, you will see that Marginal costing has an edge over Absorption costing as far as managerial decision making is concerned.

2. Absorption Costing & Marginal Costing:

 

Absorption Costing :

Absorption Costing technique is also termed as Traditional or Full Cost Method. According to this method, the cost of a product is determined after considering both fixed and variable costs. The variable costs, such as those of direct materials, direct labor, etc. are directly charged to the products, while the fixed costs are apportioned on a suitable basis over different product manufactured during a period. Thus, in case of Absorption Costing all costs are identified with the manufactured products.

This system of costing has a number of disadvantages:

1. It assumes prices are simply a function of costs.
2. It does not take account of demand.
3. It includes past costs that may not be relevant to the pricing decision at hand.
4. It does not provide information that aids decision making in a rapidly changing market environment.

Thus, the technique of Absorption Costing may lead to rather odd results particularly for seasonal businesses in which the stock level fluctuate widely from one period to another. The transfer of overheads in and out of stock will influence their profits for the two periods, showing falling profits when the sales are high and increasing profits when the sales are low.

The technique of Absorption Costing may also lead to the rejection of profitable business. The total unit cost will tent to be regarded as the lowest possible selling price. An order at a price, which is less than the total unit cost may be refused though this order, may actually be profitable.

Marginal Costing (Dec. 98, June 00, Jan. 01): Marginal costing is a special technique used for managerial decision making. The technique of marginal costing is used to provide a basis for the interpretation of cost data to measure the profitability of different products, processes and cost centers in the course of decision making. It can, therefore, be used in conjunction with the different methods of costing such as job costing, process costing etc., or even with other techniques such as standard costing or budgetary control. .

In marginal costing, cost ascertainment is made on the basis of the nature of cost. It gives consideration to behaviour of costs. In other words, the technique has developed from a particular conception and expression of the nature and behaviour of costs and their effect upon the profitability of an undertaking.

In the orthodox or total cost method, as opposed to marginal costing method, the classification of costs is based on functional basis. Under this method the total cost is the sum total of the cost of direct material, direct labor, direct expenses, manufacturing overheads, administration overheads, selling and distribution overheads. In this system, other things being equal, the total cost per unit will remain constant only when the level of output or mixture is the same from period to period. Since these factors are continuously fluctuating, the actual total cost will vary from one period to another. Thus, it is possible for the costing department to say one day that a thing costs Rs. 20 and next day it costs Rs. 18. This situation arises because of changes in volume of output and the peculiar behaviour of fixed expenses comprised in the total cost. Such fluctuating manufacturing activity, and consequently the variations in the total cost from period to period or even from day to day, poses a serious problem to the management in taking sound decisions. Hence, the application of marginal costing has been given wide recognition in the field of decision making.

3. Break Even Point & Marginal Cost:

 

Break Even Point (Dec. 99, June 02) :

The break-even point is the point or state of a business at which there is neither a profit nor a loss. In other words, it is at this point where the contribution is equal to fixed expenses.

Cash break-even point: While computing the break even point if only cash fixed costs are considered, the break even point so computed is called cash break-even point. The computation of cash break-even-point excludes depreciation and other non-cash fixed expenses. Cash break-even point thus will give such a level of output or sales at which the sales revenue will be equal to cash outflow.

Mathematically

Cash break-even point = Cash fixed costs / Contribution per unit

Composite break-even point: It is a single break-even point in the case of firms manufacturing two or more products. Composite break-even point is determined by dividing the total fixed costs by composite P/V ratio.

The composite P/V ratio can be calculated by dividing the total contribution by total sales and multiplying by 100.

Mathematically

Composite break-even point. = Total fixed costs/Composite P/V ratio

Composite P/V ratio = (Total contribution/Total Sales) x 100

Cost-break-even point: It is a situation under which the costs of operating two alternative plants are equal. Though both the plants may have the same total costs, their total fixed costs and variable costs per unit may be different. In such a case, the firm may like to determine that point at which the total costs (fixed and variable) of operating both the plants are same. Such a point may be called ‘cost break even point’.

 

Mathematically

Cost break even point = Difference in fixed cost / Difference in variable cost per unit

Alternatively: The Cost break even point can also be determined by solving the following relation for the value of X.

Cost break even point

= Fixed cost of plant 1 + [Variable cost per unit of plant 1 x X]

= Fixed cost of plant 2 + [Variable cost per unit of plant 2 x X]

‘X’ in the above relation represents cost break even point

 

Marginal Cost:  

The technique of marginal costing is concerned with marginal cost. The Institute of Cost and Management Accountants, London, has defined Marginal Cost as "the amount at any given volume of output by which aggregate costs are changed if the volume of output is increased or decreased by one unit".

Therefore, Marginal Cost refers to increase or decrease in the amount of cost on account of increase or decrease of production by a single unit. The unit may be a single article or a batch of similar articles. Marginal Cost ordinarily is equal to the increase in total variable cost because within the existing production capacity an increase of one unit in production will cause an increase in variable cost only. The variable cost consists of direct materials, direct labor, variable direct expenses and variable overheads.

The accountant’s concept of marginal cost is different from the economist’s concept of marginal cost. According to economists, the cost of producing one additional unit of output is the marginal cost of production. This shall include an element of fixed cost also. Thus, fixed cost is taken into consideration according to the economist’s concept of marginal cost, but not according to the accountant’s concept. Moreover with additional production the economist’s marginal cost per unit may not be uniform since the law of diminishing (or increasing) returns may be applicable, while the accountant’s marginal cost in taken as constant per unit of output with additional production.

 

4. Utility of Marginal Costing:

 

Q. Examine the relevance of marginal costing in the present say context of global business environment, with suitable illustrations, comparing it with other techniques. (June 02)

 

Marginal costing is a special technique used for managerial decision making. The technique of marginal costing is used to provide a basis for the interpretation of cost data to measure the profitability of different products, processes and cost centers in the course of decision making. It can, therefore, be used in conjunction with the different methods of costing such as job costing, process costing etc., or even with other techniques such as standard costing or budgetary control. The technique of marginal costing has become more relevant and useful in today's business environment of globalization. This is because in marginal costing the cost of a product, or a service is computed only on the basis of variable costs. Global companies want to take advantage of cheap labour in developing or backward countries.

Marginal costing techniques helps management in several ways in the present day context of global business environment. These are listed below:

• Volume of production: Marginal costing helps in determining the level of output which is most profitable for running concern. The production capacity, therefore, can be utilized to the maximum possible extent. It helps in determining the most profitable relationship between cost, price, and volume in the business which helps the management in fixing best selling prices for its products.
• Selecting product lines: The marginal costing technique helps in determining the most profitable production line by comparing the profitability of different products.
• Produce or procure: The decision whether a particular product should be manufactured in the factory or procured from outside source can be taken comparing the price at which it can be had from outside. In case the procurement price is lower than the marginal cost of production, it will be advisable to procure the product from outside source.
• Method of manufacturing: If a product can be manufactured by two or more methods, ascertaining the marginal cost of manufacturing the product by each method will be helpful in deciding as to which method should be adopted.
• Shut down or continue: marginal costing, particularly in the times of depression, helps in deciding whether the production in the plant should be suspended temporarily or continued in spite of low demand for the firm's products.

 Comparison of Marginal & Absorption Costing:

Absorption Costing technique is also termed as Traditional or Full Cost Method. According to this method, the cost of a product is determined after considering both fixed and variable costs. In marginal costing only variable costs are charged to production. Fixed costs are ignored. Following are differences between them.

• Recovery of Overhead: In absorption costing both fixed & variable overheads are charged to production. In contrary to this, in marginal costing only variable overheads are charged to production. Thus, in marginal costing there is under recovery of overheads.
• Valuation of stocks: In absorption costing, stocks of work in progress and finished goods are valued at works cost & total cost. In marginal costing, only variable cost is considered while computing the value of work in progress or finished products. Thus, closing stock in marginal costing is under valued as compared to absorption costing.

5. Marginal Costing: Advantages & Limitations:

 

Advantages:

1. The marginal cost remains constant per unit of output whereas the fixed cost remains constant in total. Since marginal cost per unit is constant from period to period within a short span of time, firm decisions on pricing policy can be taken. If fixed cost is included, the unit cost will change from day to day depending upon the volume of output. This will make decision-making task difficult.
2. Overheads are recovered in marginal costing on the basis of pre-determined rates. If fixed overheads are included on the basis of pre-determined rates, there will be under-recovery of overheads if production is less or if overheads are more. There will be over-recovery of overheads if production is more than the budget or actual expenses are less than the estimate. This creates the problem of treatment of such under or over-recovery. Marginal costing avoids such under or over-recovery of overheads.
3. Advocates of marginal costing argue that under the marginal costing technique, the stock of finished goods and work in progress are carried on marginal cost basis and the fixed expenses are written off to profit and loss account as period costs. This shows the true profit of the period.
4. Marginal costing helps in carrying out break-even analysis, which shows the effect of increasing or decreasing production activity on the profitability of the company.
5. Segregation of expenses as fixed and variable helps the management to exercise control over expenditure. The management can compare the actual variable expenses with the budgeted variable expenses and take corrective action through analysis of variances.
6. Marginal costing helps the management in taking a number of business decisions like make or buy, discontinuance of a particular product, replacement of machines, etc.

Limitations:

1. It is difficult to classify costs exactly into fixed and variable. Most of the expenses are neither totally variable nor wholly fixed.
2. Contribution itself is not a guide unless it is linked with the key factor.
3. Sales staff may mistake marginal cost for total cost and sell at a price, which will result in loss or low profits. Hence, sales staff should be cautioned while giving marginal cost.
4. Overheads of fixed nature cannot altogether be excluded particularly in large contracts while valuing the work-in-progress. In order to show the correct position fixed over heads should be included in work-in-progress.
5. Some of the assumptions regarding the behaviour of various costs etc., are not necessarily true in a realistic situation. For example, the assumption that fixed cost will remain static throughout is not correct.

 

6. Practical Problems:

 

Q. Rajkumar Ltd. provides you the following information: (June 03):

	Sales (Rs.)	Profit (Rs.)
Period 1	10,000	2,000
Period 2	15,000	4,000

You are required to calculate:

• P/V ratio
• Fixed cost
• Break-even sales volume
• Sales to earn a profit of Rs. 3,000 and
• Profit when sales are Rs. 8,000

Solution:

i)

	Change in profit
P/V ratio  =		x	100
	Change in rate

 

	2000
=		x	100	=	40%
	5000

ii)

Fixed Cost = Contribution - Profit

	10000
=		x	40 - 2000	=	2000
	100

iii)

	Fixed Cost
Break-even sales volume =
	P/V ratio

 

	2000
=		X	100
	40

= 5000

iv)

	Fixed cost + Profit
Sales =
	P/V ratio

 

	2000 + 3000
Sales =
	40%

= 12500

v)

Profit = Sales - Variable cost - Fixed cost

Variable cost = 8000 x (60/100) = 4800

Profit = 8000 - 4800 - 2000 = 1200

Q. From the following information relating to Smith sons, calculate the break-even point and the turnover required to earn a profit of Rs. 3,00,000 (Dec. 02)

 

 

 

Solutions:

 

Selling price	= 50
Less variable cost	= 20
Contribution	= 30

 

	Fixed cost
BEP in units =
	Contribution per unit

 

	2,10,000
=		=	7,000 units
	30

 

	2,10,000
BEP in amount =		=	3,50,000
	60%

Calculation of turnover to earn a profit of Rs. 3,00,000

	Fixed cost + Desired Profit
Sales =
	Contribution per unit

 

	21,000 + 3,00,000
=
	30

= 17000 units

	Fixed cost + Desired Profit
Sales (amount) =
	P/V ratio

 

	21,000 + 3,00,000
=
	60%

= 8,50,000

Margin of Safety

Margin of safety = Total sales - sales at BEP

MOS (Amount) = 850000 - 350000 = 500000

MOS (Units) = 17000 - 7000 = 10000 units

> For theory part please refer to chapter 9.

Q. Premier Ltd. produces a standard article. The results of the last four quarters of the year 2000 are as follows: (Dec. 01)

Quarters	Output (unit)
I	1,000
II	1,500
III	2,000
IV	3,000

The cost of direct material is Rs. 30 and direct labour is Rs. 20 per unit. Variable expenses are Rs 10 per unit. Fixed expenses are Rs 6,000 per annum. (i) Find out full cost percent for each quarter. (ii) Find out BEP (Break Even Point) in units for each quarter if selling price is Rs 100 per unit and the entire output is sold.

Solutions:

 

	I	II	III	IV
Output	1000	1500	2000	3000
Direct material Rs. 30	30000	45000	60000	90000
Direct Labour Rs. 20	20000	30000	40000	60000
Variable Expenses Rs. 10	10000	15000	20000	30000
Fixed Expenses	1500	1500	1500	1500

Annual expenses = 6000

Quaterly expense = 6000/4 = 1500

i) Full cost percent for each quarter

Total	61500	91500	121500	181500
Percentage	13.5	20	26.7	39.80

ii) BEP in units

BEP = Fixed cost/ contribution per unit

Contribution = Sales - Variable cost

= 100 - (30 + 20 + 10)

= 40

BEP = 6000/40 = 150 units

 

Q. From the following data : (June 01)

Selling Price = Rs. 40 per unit

Variable manufacturing cost = Rs. 20 per unit

Variable selling cost = Rs. 10 per unit

Fixed factory overheads = 10,00,000 per year

Fixed selling costs 4,00,000 per year

Calculate : i) Break-even point expressed in rupee sales. ii) Number of units that must be sold to earn a profit of Rs. 2,00,000 per year.

Solutions:

 

i)

Contribution = Sales - variable cost

= 40 - (20 + 10)

= 10

Total fixed cost = Fixed factory overheads + Fixed selling cost

= 10,00,000 + 4,00,000 = 14,00,000

	Fixed cost
BEP in units =
	Contribution per unit

 

	14,00,000
=
	10

= 1,40,000 units

BEP (Value) = Fixed cost/(P/V ratio)

	Contribution
P/V ratio  =		x	100
	Sales

= 10/40 X 100 = 25%

BEP (value) = (14,00,000/25) X 100

= 56,00,000

ii) Number of units must be sold to earn a profit of Rs. 2,00,000 per year

	Fixed cost + Desired Profit
Sales =
	P/V ratio

= (14,00,000 + 2,00,000) / 25%

= 64,00,000

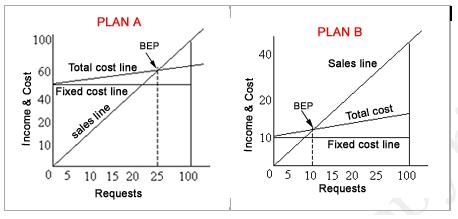
Q. A medical advisory service offers to its subscribers complete information on doctors, paramedicals, health insurance, super speciality hospitals and general health awareness. It now plans to computerise these sevices and has a choice of two systems on which to offer these services. Under option A, a computer system would be leased for Rs. 50 lakhs per year and the subscriber requests would be processed with avariable cost of Rs. 20 per request. Under plan B, a computer system would be leased for Rs. 10 lakhs per year and the subscriber requests would be processed with a variable cost of Rs. 120 per request. Under either option, the subscriber can and is happy to pay Rs 220 per request that is processed. On the basis of this data

(i) Which option is more risky?

(ii) Draw break even charts for both options.

(iii) At what volume of business would the operating profit under either option be the same?

(iv) Which plan has a higher degree of operating leverage?

 

 

Solutions:

PLAN A

BEP (units) = Fixed costs/contribution per unit

= 50,00,000/(220 - 20)

= 25,000 requests

 PLAN B

BEP (units) = Fixed costs/contribution per unit

= 10,00,000/(220 - 120)

= 10,000 requests

Plan is more risky because initial fixed cost is very high. If sales fall below 25,000 requests, losses will be incurred.

(ii) Break even chart

iii) Profit under plan A = (Price - Varaible cost) X Units - FC

= (220 - 20) X (x) - 50,00,000

Profit under plan B = (220 - 120) X (x) - 10,00,000

Equating both the equations we get

(220 - 20) X (x) - 50,00,000 = (220 - 120) X (x) - 10,00,000

100x = 40,00,000

x = 40,000 requests

iv) Operating Leverage

Degree of operating leverage = %change in net operating income / % change in units sold or sales

= Contribution/EBIT

Where EBIT is Earning before interest & tax

In both the plans the contribution is calculated taking hypothetical data of 50,000 requests because the question does not provide any information.

 PLAN A

	50000 X (Rs. 220 - Rs. 20)
=
	50000 X (220 - 20) - Rs. 50,00,000

= 2

 PLAN B

	50000 X (Rs. 220 - Rs. 120)
=
	50000 X (220 - 120) - Rs. 10,00,000

= 1.25

Plan A has greater operating leverage owing to higher fixed costs.