APPLICATIONS
Term-End Examination
December, 2OO7
CS-62 : C PROGRAMMING AND DATA STRUCTURE
Time: 2 hours Maximum Marks : 60
Note : Question no. 1 is compulsory. Answer any three questions from the rest. All algorithms should be written nearer to 'C' Language.
l. (a) Define an AVL tree. Construct a height balanced tree for the following list of elements : (8)
4 , 6 , 12 , 8 , 4 , 2 , 15 , 7 , 3
(b) Write an algorithm to implement linked list using pointers and perform the following tasks : (10)
(i) Delete a node in the list, given a pointer to that node
(ii) Write a function to reverse the linked list.
(c) Write an algorithm that reads m x n matrix "A" and p x q matrix "B", checks whether these matrices are multipliable in either order or not(eg. whether AxB or BxA is defined). Further , if AxB or BxA is defined then calculate the product.
Note : Show proper error handling also. (7)
(d) Calculate the time complexity of the following code
by using Big 'O' notation : (5)
1. Scanf ("%d" , &n);
2. Scanf ("%d",&m)
3. for (i=0; i<=m+n; i+=2)
4 . Printf ("%d n", i- 1);
5. for (j=m*n/100; j<=m*n; j++)
6. Printf ("%d
", j);
2. (a) Write an algorithm, that accepts 12 words of
different string-size
characters in the string
e.g. : If string is "ABFD", its ASCII mapping is
65, 66, 70, 68 respectively and sum is
6 5 + 6 6 + 7 0 + 6 8 : 2 6 9
Hint: ASCII value of 'A' starts with 65, and 'a' (6)
6 starts with 97 .
(b) Write an algorithm to implement bubble sort technique. Also, show the steps of bubble sort on the (4)
following given number :
"5, 12.,39, 7, 3, 19, 69, 115"
3. (a) Construct the binary tree using the following preorder and inorder sequences:
Preorder : A B C E I F J D G H K L
Inorder : E I C F J B G D K H L A
Also, write the postorder sequence of it. (5)
(b) Write algorithms to perform the following operations (5)
in circular queue :
(i) Create a circular queue
(ii) Check whether a queue is empty
(iii) Insert an element in a queue
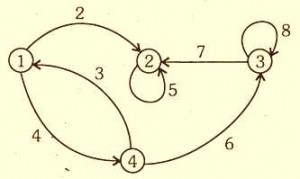
4. (a) Consider the following graph :
Make the adjacency matrix for the given graph.
Also, write an algorithm to compute the transpose
of the matrix. (5)
(b) What is a sparse matrix ? Which method is used to represent its non-zero elements ? Also,write the algorithm corresponding to this method,explaining its steps (5)
5. Explain the following with an example of each : (10)
(a) Direct file organisation
(b) Depth first search
(c) B-tree
(d) Column major order