Q. 4 Solve the following systems of simultaneous linear equations using Gauss elimination method and Gauss-Seidel Method.
(i) 2x4+3x2+7x3=12
4x1+5x2-12x3= -3
x1- 4x2+5x3=12
Solution:
By Gauss elimination,
We consider the Augmented [A|b] and perform the elementary row operation on the augmented matrix
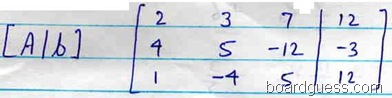
The first step is to use first equation to eliminate the unknown x1 from second , third equation. This is accomplished by performingR2 – 2R1 and R3 – ½ R1. This gives the derived system as
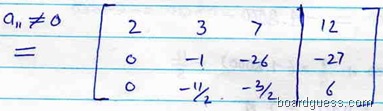
By performing the operation R3 – 11/2 R2 . The resulting system is
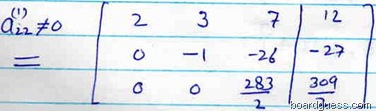
This is the final equivalent system
2x1+3x2+7x3 = 12
-x2 - 26x3 = -27
283/2 x3 = 309/2
By equation 1,2 and 3
The solution is
x1 = 309/283, x2 = - 309/283 and x3 = 1206/283
By Gauss – Seidel Method,
X1(k+1) = - 3/2 x2(k) – 7/2x3(k) + 6
X2(k+1) = - 4/5 x1(k+1) + 12/5 x3(k) - 3/5
X3(k+1) = - 1/5 x1(k+1) + 4/5 x2(k+1) + 12/5
Letting (x0) = (0,0,0)T we have from first equation
X1(1) = 6.0000
X2(1) = - 4/5 x 8.0000 – 3/5 = - 5.4000
X3(1) = - 1/5 x 6.0000 + 4/5 x (- 4.8000) + 12/5 = 2.6400
(x1) = (6.0000, - 5.4000, 2.6400)T
(x4) = (1.0918, - 1.3886, 4.2614)T
(ii) x1+2x2+3x3=8
4x1- 6x2+3x3= -5
2x1+4x2+9x3=19
Solution:
By Gauss elimination,
We consider the Augmented [A|b] and perform the elementary row operation on the augmented matrix
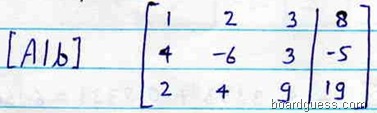
The first step is to use first equation to eliminate the unknown x1 from second , third equation. This is accomplished by performingR2 – 4R1 and R3 – 2R1. This gives the derived system as
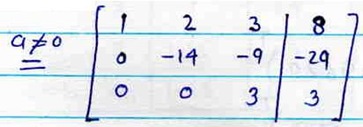
This is the final equivalent system
x1+2x2+3x3=8
-14x2 - 9x3 = -29
3x3 = 3
By equation 1,2 and 3
<<Previous Answer || Index Assignment || Next Answer>>