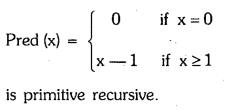Term-End Examination
June, 2006
CS-73 : THEORY OF COMPUTER SCIENCE
Time : 3 hours Maximum Marks : 75
Note : Question number 1 is compulsory. Attempt any three questions from the rest.
1. (a) What is a linear bounded automaton (LBA) ? What is the class of languages it can accept?(4)
(b) Languages L1 and L2 are both recursive. Is their intersection also recursive ? Justify your answer.(5)
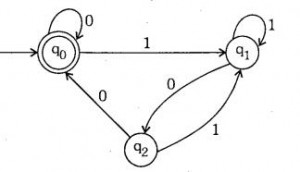
(c) Find a regular expression for the following finite automata. (5)
(d) What is Ld, the diagonal language ? Is it decidable ? Give reasons. (5)
(e) Differentiate between Moore and Mealy machines. (3)
(f) Describe the little-oh and little-omega growth rate functions. (4)
(g) Show that the predecessor function
2. (a) Combine CFG and BNF to define the syntax of an assignment statement. (6)
(b) When is a problem NP-complete ? Give an example of an NP-hard problem which is not NP-complete.Justify your example. (5)
(c) State and prove the pumping lemma for context free languages.(4)
3. (a) Design a pda (push down automaton) for the following context free grammar. (5)
S - aAA
A - aSIbSIa.
(b) Is the language L = {a' bi I i * j} regular ? Justify your answer. (6)
(c) Describe two ways in which a pda can accept a context free language. (4)
4. (a) Design a Turing Machine which accepts the language
L= {an b° I n> 1} 6
(b) What is the halting problem in the context of Turing
Machines ? Prove that this problem is undecidable. 5
(c) Describe the working of a multi-tape Turing Machine. 4
5. (a) Prove that the following decision problem is undecidable :
Given a Turing Machine T, is. L(T) non-empty ? (6)
(b) Prove that the regular languages are closed with respect to concatenation. (2)
(c) Prove that the independent-set problem is NP-complete by reducing the vertex cover problem
to it. (7)