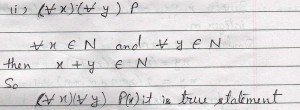Q1:
a) Make truth table for :
######Solution Start#######
(i)
|
p |
q |
r |
r’ |
p+r’ |
(p+r’)*p |
(p+r’)*p+q |
qà(p+r’)*p+q |
|
T |
T |
T |
F |
T |
T |
T |
T |
|
T |
T |
F |
T |
T |
T |
T |
T |
|
T |
F |
T |
F |
T |
T |
T |
T |
|
T |
F |
F |
T |
T |
T |
T |
T |
|
F |
T |
T |
F |
F |
F |
T |
T |
|
F |
T |
F |
T |
T |
F |
T |
T |
|
F |
F |
T |
F |
F |
F |
F |
T |
|
F |
F |
F |
T |
T |
F |
F |
T |
(ii)
|
p |
q |
r |
r’ |
q*p |
q*p+r’ |
q+q*p+r’ |
pà q+q*p+r’ |
|
T |
T |
T |
F |
T |
T |
T |
T |
|
T |
T |
F |
T |
T |
T |
T |
T |
|
T |
F |
T |
F |
F |
F |
F |
F |
|
T |
F |
F |
T |
F |
T |
T |
T |
|
F |
T |
T |
F |
F |
F |
T |
T |
|
F |
T |
F |
T |
F |
T |
T |
T |
|
F |
F |
T |
F |
F |
F |
F |
T |
|
F |
F |
F |
T |
F |
T |
T |
T |
######Solution End########
b) Explain with example the use of conditional connectives in the forming of prepositions. (2 Marks)
=========Solution Start here=========================
Conditional Connectives: Give any two preposition p and q, we denote the statement 'If p, then q' by p --> q. we also call p the hypothesis and q the conclusion. Further a statement of the form p -->q is called a conditional statement or a conditional preposition.
Example: The conditional proposition If m is in Z, then m belongs to Q'. The hypothesis is 'm belong Z' and the conclusion is 'm belong Q'.
Mathematically, we can write this statement as
m belong Z --> m belong Q.
===========Solution End here========================
c) Write down suitable mathematical statement that can be represented by the following symbolic properties.
=============Solution Start here=====================
Suitable mathematical statement that can be represented by following symbolic properties.
==============Solution End here=====================
===================
Assignment Index | <<Previous Answer | Next Answer>>
===================