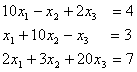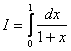Q.1 (a)

Write a program in C to find a root using Secant Method. Perform the five iterations to obtain the smallest positive root of the equation f(x) = cos x – xe^x = 0,, verify your answer with the program written by you.

Q.1 (b)

Out of the three methods i.e. Secant method, Regula Falsi method and the Newton Raphson method which method is more efficient and why? Determine the efficiency or the order of these three methods?

Q.1 (c) Solve the equations:

Using the LU decomposition method.

Q.1 (d)

Consider the system of equations given below. Use the Jacobi iterative method and perform three iterations.

Q.2 (a)

Find the unique polynomial of degree 2 or less, such that f(0)=1, f(1)=3, f(3)=55, using the Lagrange interpolation? Write a program in C evaluating the polynomial using Lagrange interpolation.

Q.2 (b)

Compute the integral by applying Gauss’s Quadrature formula.

Q.2 (c)

Using Runge-kutta method obtain y when x=1.1, given that y=1.2 when x=1 any y satisfies the equation.

Dy/dx=3x²+y².

Q.2 (d)

Evaluate the integral

Using (i) composite trapezoidal rule, (ii) composite Simpson’s rule, with 2, 4 and 8 equal subintervals.

Q3: (a)

Find the probability of getting between 6 and 9 tails inclusive in 20 tosses of a fair coin by using (i) the binomial distribution, (ii) the normal approximation to the binomial distribution.

Q.3 (b)

Table 2 below shows the respective heights x and y of a sample of 12 fathers and their oldest sons. (i) Construct a scatter diagram. (ii) Find the least-squares regression line of y on x. (iii) Find the least-squares regression line of x and y.

Table 2

Height x of Father (centimeters)	165 160 170 163 173 158 178 168 173 170 175 180
Height y of Son (centimeters)	173 168 173 165 175 168 173 165 180 170 173 178

Q.3 (c)

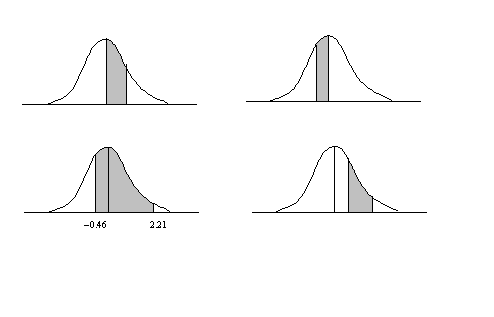
Find the area under the standard normal curve (a) between z = 0 and z = 1.2, (b) between z = – 0.68 and z = 0, (c) between z = – 0.46 and z = 2.21, (d) between z = 0.81 and z = 1.94.

Free Solutions:

• Economics Set-2 (2008)
  (203 downloads)