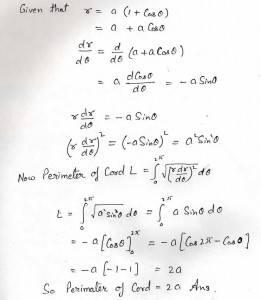Q1. Trace the following curve
y=x/(1+x2) (5 Marks)
Solution:
Given that y=x/(1+x2)
therefore y(1+x2) = x
therefore y + x2y = x
therefore dy/dx + x2 (dy/dx) + 2xy = 1
therefore dy/dx(1+x2) = 1 – 2xy
Putting the value of y
dy/dx(1+x2) = 1 – 2x[x/(1+x2)]
= 1 – 2x2/(1+x2) = [1 – x2 / 1 + x2]
therefore dy/dx = [1 – x2 / (1 + x2)2]
From eqn(1) y=x/(1+x2)
So if y=0 and x=0
Then f(x,y) = y - x/(1+x2) = 0
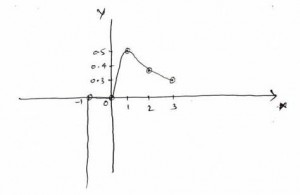
Then curve
|
Y |
0 |
0.5 |
0.4 |
0.3 |
Infinite |
|
x |
0 |
1 |
2 |
3 |
-1 |
Curve is traced as follow
Q2. Obtain fifth roots of 4+3i. (5 Marks)
Solution:
Given Complex number is Z = 4 + 3i
Q3. Prove that |4x – 5y| <= 4|x| + 5|y| (5 Marks)
Solution:
L.H.S = |4x – 5y|
= (|4x – 5y|2) (because |x|2 = x for all x belong R)
= (4x – 5y)
Therefor |4x|2 + |5y|2 – 2|4x|.|5y|
= > (|4x| + |5y|)2 - 2|4x|.|5y|
Since |x|>= 0 for all x belong R
So taking square on both side
|4x – 5y| <= 4|x| + 5|y|
Given equation is
5x3 – 8x2 + 7x + 6 = 0
= > x3 – (8/5)x2 + (7/5)x + (6/5) = 0 -----------(1)
Let a, b, c are the roots, so
a + b + c = 8/5 -------------------(2)
ab + bc + ca = 7/5 --------------------(3)
abc = -6/5 --------------------(4)
Now Let roots of cubic equation is p, q, r such that
p = a2 + b2 + ba -------------------(5)
q = b2 +c2 + cb ---------------------(6)
r = c2 + a2 + ca --------------------(7)
Then cube equation is
(x - p)(x - q)(x - r) = 0
= > (x - p)[x2 – (q + r)x + qr] = 0
= > x3 – x2 (p+q+r) + x(pq+qr+rp) – pqr = 0 ------------(8)
Now (p+q+r) = 2(a2 + b2 + c2) + ab + bc + ca
= > (p+q+r) = 2[(a + b + c)2 – 2(ab + bc + ca)] + ab + bc + ca
= > (p+q+r) = 2(a + b + c)2 – 3(ab + bc + ca)
= > (p+q+r) = 2(8/5)2 – 3*(7/5)
= > (p+q+r) = 23/25 -----------------------(9)
Similarly, pq+qr+rp = (a2 + b2 + ab)(b2 + c2 + bc)
= a2b2 + a2c2 + a2bc + b4 + b2c2 + b3c + ab3 + abc2 + ab2c
We can use,( a2 + b2 + c2)2 = a4 + b4 + c4 + 2(a2b2 + b2c2 + c2a2)
Write equation in term of a2, b2 and c2
Putting the value from (5), (6) and (7) we get
pq+qr+rp = 22/25 -------------------(10)
and pqr = -21/25 --------------------(11)
putting the value of (9), (10) and (11) in (8)
= > x3 – x2 (23/25) + x(22/25) – (-21/25) = 0
= > 25x3 – 23x2 + 22x – 21 = 0
Q5. Find the perimeter of the cord
Solution: