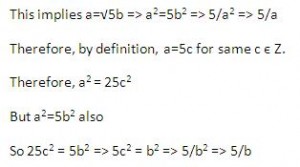Q2.
(a). Explain different methods of proof with the help of one example of each. (6 Marks)
------------------Solution Start ----------------------------
Different Methods Of Proof:
1. Direct Proof A direct proof of p=>q is a logically valid argument that begins with the assumptions that p is true and, in one or more applications of the law of detachment, concludes that q must be true.
So, to construct a direct proof of p=>q, we start by assuming that p is true. then, in one or more steps of the form p=>q1, q1=>q2,....qn=>q, we conclude that q is true.
Example: The product of two odd integers is odd.
Solution: Let two odd integers x and y.
So the hypothesis, p: x and y are odd.
The conclusion we want to reach q: xy is odd
we will first proof that p=>q.
since x=2m+1 for some integers m.
similarly, y=2n+1 for some integers n.
then xy=(2m+1)(2n+1) = 2(2mn+m+n)+1
therefor xy is odd.
So, we have since that p=>q.
2. Indirect Proofs We shall consider two roundabout method for proving p=>q.
Proof by contra positive: In the first method, we we use the fact that the proposition p=>q is logically equivalent to its contra positive (~q => ~p) ,
What we do to prove p => q in this method is to assume that q is false and then show that p is false.
Example: Prove that 'If x, y belong Z such that xy is odd then both x and y are odd'.
Solution: p: xy is odd.
q: both x and y is odd, then
~p: xy is even.
~q:both x and y is even.
We want to prove p=>q, by proving that ~q=>~p. So we start by assuming that ~q is true, we suppose that x is even.
The x = 2n for some n belong N
therefor xy=2ny
therefor xy is even, that is ~p is true.
So ~q=>~p therefor, p=>q.
Proof by contradiction: In this method, we prove q is true, we start by assuming that q is false (~q is true). Then by a logical argument we arrive at a situation where a statement is true as well as false, we reach contradiction r ^ ~r for some statement that is always false. This con only happen when ~q is false also. therefor q must be true. This method is called Proof by contradiction.
Example: If two distinct lines L and L' intersect , then their intersection consists of exactly one point.
Solution: There is two distinct line L and L' intersect more then one points. Let us call two of these distinct points A and B. Then , L and L' contain A and B. this contradicts the axiom from geometry that says 'Given two distinct points , there is exactly one line containing them.'
Therefor if L and L' intersect then they must intersect in only one point.
3. Counterexamples Counterexample to a statement p proves that p is false that is ~p is true.
Example: Proof that For All x belong Z, where x belong Q/N.
Solution: To disproving p <=> q it is enough to proof that p <=> Q is false or q=> p is false.
------------------Solution End -----------------------------
(b). Show whether root 17 is rational or irrational. (4 Marks)
---------------------Solution Start------------------------
Root17 is irrational, since 17 is a prime.
because Square root of any prime number is irrational.
Proof BY Contradiction,
We begin by assuming that root 17 is rational. This means that there exist positive integers a and b such that root 17 = a/b , where a and b have no common factors.
But now we find that 17 divides both a and b, which contradicts our earlier assumption that a and b have no common factor.
Therefor, we conclude that our assumption that root 17 is rational is false, that is root 17 is irrational.
---------------------Solution End-------------------------