(a). Draw a Venn diagram to represent followings:
i) (A B) U (C~A)
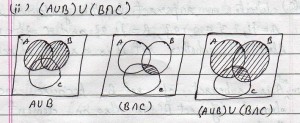
ii) (A B) U (B ~ C) (4 Marks)
=============Solution Start here======================
Draw a Vann diagram to represent following:
=============Solution End here======================
(b). Give geometric representation for the following:
i) { 3, 1} x R
ii) {-1, -1) x ( -2, 3) (4 Marks)
=============Solution Start here====================
Geometric representation: (i) {3,1} x R => {3} x R and {1} x R
The geometric diagram for {3} x R will be the line parallel to Y axis, x=3.
And similarly x=1, parallel to y axis.
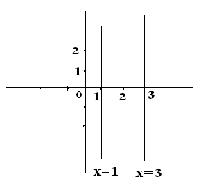=============Solution End Here=====================
(c). What is principle of strong mathematical induction? In which situation this principle is used. (2 Marks)
======================Solution Start here=============
Principle of Strong Mathematical Induction:
Let P(n) be a predicate that involves a natural number n. Suppose we can show that
(i) p(m) is true for some m belong N
(ii) whenever p(m) ,p(m+1),.........,p(k) are true,
That p(k+1) is true, where k>=m we can conclude that p(n) is true for all natural number n>=m.
In the induction step we are making more assumption. That p(n) is true for every n lying between m and k , not just that p(k) is true.
To use the strong form of the PMI, we take m=1. We have seen that p(1) is true We also need to see if p(2) is true.
Then next step,
For an arbitrary k>=2 , We assume that p(n) is true for every n such that,
=================Solution End Here===================