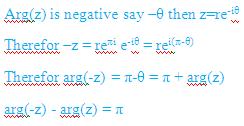Important Question Mathematics And Statistics with Hints

1. If iz³+z²-z+i=0, Then |z| is equal to

(a) -1 (b) 1 (c) i (d) –i

2. If arg (z)<0, then arg(-z) – arg(z) is equal to

3. For any complex number z, the minimum value of |z|+|z+1| is

(a) 1 (b) 0 (c) 1/2 (d) 3/2

4. If z₁, z₂, z₃ are in H.P. they lie on a

(a) circle (b) sphere (c) straight line (d) none of these

5. If z⁴ = i then z can take the value

6. The least value of |z+(1/z)| if |z| >= 3 is

(a) 10/3            (b) 8/3          (c) 4/3              (d) 2

7. The harmonic mean of the roots of the equation

(a) 2           (b) 4               (c) 6                       (d) 8

8. Let the positive number a, b, c ,d be in A.P. then abc, abd, acd, bcd are

(a) Not a A.P./ G.P./ H.P. (b) in A.P. (c) in G.P. (d) in H.P.

9. The sum of all two digit number witch are odd is

(a) 2475 (b) 5049 (c) 2530 (d) 4905

10. The harmonic mean of two is 4, their A.M. is A, and G.M. is G satisfy the relation 2A + G² = 27. The two number are

(a) 6, 3 (b) 5, 4 (c) 5, -2.5 (d) -3, 1

11. If x² – 3x + 2 is a factor of x⁴ – px² + q = 0, then (p, q) are

(a) (4, 5) (b)(5, 4) (c) (2, 3) (d) (0, 0)

Answer

1. (b) 2. (a) 3. (a) 4. (c) 5. (a) 6. (b) 7. (b) 8. (d) 9. (a) 10. (a) 11. (b) 12. (a) 13. (d) 14. (c) 15. (a)

Solution (Hint) of these question:

Ans-1

Dividing by I then z³+(1/i)z²-(1/i)z+1=0

We know that (1/i)=-i

z³-iz²+iz+1=0 or z² (z-i)+i(z-i)=0 as 1=-i²

or (z-i) (z²+i)=0 therefor z=i or z²=-i

therefor |z| = |i| = 1 and | z²| = |z|² = |-i| = 1

therefor |z| =1

hence in either case |z|=1

Ans-2

Ans-3

1 = z + (1-z)

|1| = | z + (1-z)| <= |z| + |1-z|

= | z + (1-z)|

Therefor | z + (1-z)| >= 1

Therefor minimum value is 1.

Ans – 4

z₁, z₂, z₃ are in H.P. means that their moduli r₁, r₂, r₃ are in H.P.

Ans – 8

a, b, c ,d are in A.P. then dividing by abcd

1/bcd, 1/acd ,1/abd, 1/abc are in also in A.P.

Hence there reciprocals are in H.P.

Ans – 9

11+13+15+……..+99

A=11, d=2, n=45

Ans – 10

H=4 and G²=AH gives G² =4A

Also 2A+G²=27 or 2A+4A=27

2A=9 or a+b=9 ——-(1)

Also G²=4A=18 or ab=18 —–(2)

By eq (1) and (2)

t² – 9t + 18 =0

Therefor, t=6, 3

Ans – 11

x² – 3x + 2 = (x-1)(x-2)

therefor, 1 and 2 are root of 2^nd equation

q-p+1 = 0, q-4p+16 =0

p=5, q=4

Ans – 12

b²=ac => 2logb =loga + logc

therefor, log_na, log_nb, log_nc are in A.P.

Their reciprocals

log_an, log_bn, log_cn are in H.P.

Ans – 13

(2n)!/{3!(2n-3)!} *{2!(n-2)!}/n! =11/1

=> 4(2n-1) = 33

Therefor, n = 37/8

Ans – 14

¹⁰P₉ – ⁹P₈ =10! – 9!

= 9!(10-1) = 9*9!

Ans – 15

2³ⁿ = 8ⁿ = (1+7)ⁿ

=> (1+7)ⁿ – 7n – 1 = ⁿC₂ 7² + ⁿC₃ 7³ + …..

=> 7²

Hence divisible by 49